Clarifications | Rules vs Exceptions

A common rhetorical device everyone has been guilty of using at some point is referencing an exception as a rule: taking an uncommon example or scenario to disprove a common one. In some instances, it’s essential to highlight certain exceptions to point out flaws in logic or argumentation. However, one can easily use this thought process to justify their biases by ignoring generalities in favor of specifics—no matter how rare. There are two reasons why this rhetoric still occurs: firstly, to avoid stereotyping and, secondly, to discredit one’s reasoning by focusing on the pejorative double standards of an argument rather than offering a valid counterpoint, also known as a whataboutism.
Stereotyping is when one categorizes a group based on a particular set of (often negative) beliefs or assumptions they’ve developed. Stereotypes can range from mildly insulting to downright defamatory and can be subtle or explicit. For example, the verb gyp, which means to cheat/swindle, derives from the word Gypsy. Gypsy was a label created by Europeans to refer to the Romani people, who they mistakenly believed originated from Egypt due to their dark complexion. The negative connotations surrounding Gypsies affected public perceptions about the Roma that were not only harmful but prejudicial, creating stereotypes that suggested that all Gypsies were grifters. Today, to call someone a gyp or to say one has been gypped is to perpetuate the stereotype. Hence, why many avoid generalizing others to begin with—they don’t want to stereotype someone based on false assumptions.
However, generalizations serve a purpose. They help to quickly assess an individual based on as little observational information as possible. While not all generalizations are true, it does not mean that all generalizations are, therefore, false. If there is evidence to support generalities surrounding sex, race, or other immutable characteristics, then it is not stereotyping but observing that there are distinctions between different people. In other words, all stereotypes are generalities, but not all generalities are stereotypes.
Such distinctions, however, lead one into taboo territory. Scientific research on sex and race is highly controversial in most intellectual circles. One example was the 1994 publication of The Bell Curve by psychologist Richard J. Herrnstein and political scientist Charles Murray. They both argued, in one chapter, that there was a correlation between race and intelligence. Many prominent intellectuals, such as Stephen J. Gould and Noam Chomsky, have criticized the book for being biased towards a genetic basis for intelligence while ignoring environmental factors. Even now, the book incites debate among scholars who, depending on one’s views of race and sex differences, will defend or attack it. Given the stark contrast of ideas, it is no wonder why there is no consensus on the subject. The conundrum one faces when entering the debate is if one acknowledges differences between races or sexes, then they are accused of being either racist or sexist. On the other hand, if one dismisses differences or views them as negligible, then they are criticized as being either ignorant or intellectually dishonest; hence, why I must preface the distinction between a generality and a stereotype and how it relates to rules and exceptions.
Since I primarily discuss sex differences, I must explain what I mean when I state, “Men are this and women are that,” before I am accused of stereotyping. While most acknowledge that men and women are different, many will downplay those differences by referencing an exceptional man or woman who does not fit the conventional role in order to offset the generalities people have about the sexes. However, when taken to extremes, it gives the false impression that men and women are mostly the same, if not identical. To the point that anyone who thinks otherwise is negatively discriminating against women. In other words, generalizing men and women is the same as stereotyping all men and women and, thus, is sexist. Needless to say, this logic is flawed for two reasons. Firstly, generalities do not stereotype individuals but clarify differences between them. Secondly, similarities between men and women do not invalidate distinctions. Based on the current data, it is clear that men and women act in a way that is conducive to their sex and is influenced by a complex series of gene-environment interactions. When comparing both sexes separately, there is a disparity between men’s and women’s behaviors that leads them to take on more conventional roles. When juxtaposed together, men and women are, on average, the same but have statistically significant differences on the extremes. Herein lies the confusion with sex differences—there is a giant overlap between both sexes. Yet, scientific research shows greater variance in men than women, a phenomenon supported by evolutionary theory.
Getting back to why exceptions do not disprove the rule, we must first examine how rules are determined. And the only way we can do that is by understanding statistical averages. In mathematics, the average (also known as the mean) is the sum of values divided by the number of total values. For example, if you wanted to measure the average height of a group of 5 people, you would begin by measuring each of them individually, adding up their values, and then dividing them by the total number of people counted, in this case 5. So, if the results are 5’1”, 5’4”, 5’5”, 5’, and 5’7”, then the average height would be 5’3”.
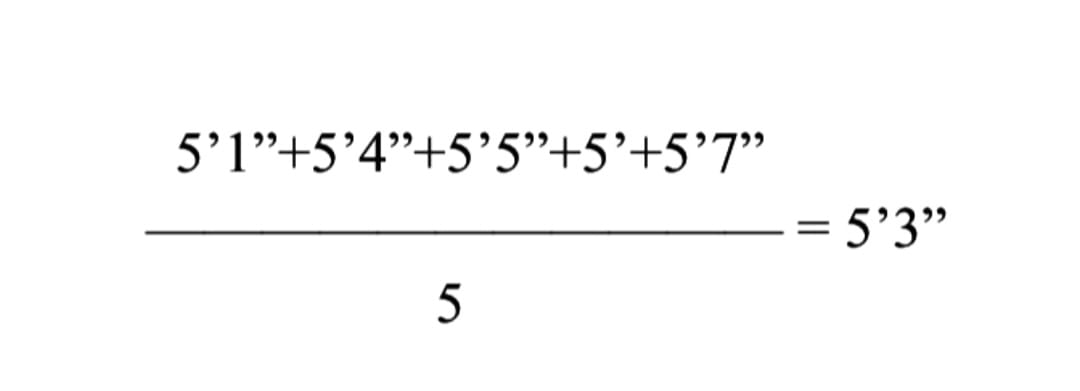
Averages are a fact of life and exist throughout Nature. It is averages that made the publication of The Bell Curve possible. Of course, the shape of a bell curve can vary depending on the size and spread of the data points being measured. Thus, some have a more prominent curvature than others, depending on the standard deviation. The standard deviation, which determines the width of the curve, is the variation or dispersion of a set of values in relation to the average. A low standard deviation indicates that the data is clustered closer to the average. A high standard deviation indicates that the data is spread over a wider range of values.
When analyzing statistical data, it is important to scrutinize how the researchers conducted the study, what sample sizes they used, the potential biases of the samples, and how they calculated the averages. To determine rules and exceptions, one must run several tests to find consistencies within the data. If a pattern emerges and the results are, on average, the same, then such a pattern can be considered a rule. Of course, rules can change over time if those changes are statistically significant. A mistake people will often make is using an exception as proof of statistical significance when, in actuality, it proves the opposite by establishing that a rule must exist in the first place. In other words, the exception proves the rule because for there to be exceptions, there must be an average from which to deviate.
Taking our previous example, if the average height of 5 people is 5’3”, we would assume little variation, expecting a low standard deviation. However, if the details of the results revealed that one of those individuals was an NBA athlete while the rest suffered from dwarfism, then we would have a different picture overall of what is considered the average height. We can even apply the same concept to the average yearly wage using the same five people. Suppose the average salary was $50,000 a year. Again, we imagine each individual making a little less or more than $50,000. But if it were revealed that the NBA athlete makes over six figures while the rest of the dwarves live in poverty, then we can disregard the calculation of the average based on the mean and instead determine it either by finding the middle number of all the values (also known as the median) or finding the most frequently repeated values (also known as the mode.)
This is why statistics can be misleading when establishing rules and exceptions. Depending on who is presenting the information, it can essentially say anything one wants to say while substantiating their claims behind an impenetrable wall of numbers and figures that most people would not even take the slightest effort to try and penetrate. Or as the author Darrell Huff stated in his best-selling book “How to Lie With Statistics:”
“The secret language of statistics, so appealing in a fact-minded culture, is employed to sensationalize, inflate, confuse, and oversimplify. Statistical methods and statistical terms are necessary in reporting the mass data of social and economic trends, business conditions, ‘opinion’ polls, the census. But without writers who use the words with honesty and understanding and readers who know what they mean, the result can only be semantic nonsense.” ¹ - Darrell Huff
While statistics can be useful for understanding all manner of phenomena, we must be careful not to assume that the data points in a direction favorable to our biases. Instead, we should start by determining what the rules and exceptions are from the evidence gathered. Moreover, we must not shy away from generalizing out of fear that we will be accused of stereotyping. Rules and exceptions exist as a consequence of nature and cannot be ignored, denied, or reinterpreted to fit a different narrative. In other words, exceptions cannot disprove the rule. Outliers cannot invalidate averages. Some generalities exist and need to be acknowledged to remain objective. However, it is essential that, despite these generalities, we do not assume a person is guilty by association, which means we must reserve judgment and look at individuals on a case-by-case basis. Clearly, some factors can be easily overlooked when drawing conclusions about statistical averages, and it doesn’t help that they can be misinterpreted or manipulated to skew public perception—an all too common occurrence among debating scholars and politicians who wish to build a false narrative. A fact emphasized by author Mark Twain, who once remarked that
“There are three kinds of lies: lies, damned lies, and statistics.” ² - Mark Twain
If we are to interpret what the rules and exceptions are correctly, we must first identify what the average is and, correspondingly, what the outliers are. We must also decide the best way to find the average, whether using the mean, median, or mode. Depending on the question, one of those methods will give us the best answer. Using our previous example on average height, if the majority of the people in the test sample are poverty-stricken dwarves while one member is a tall, wealthy NBA athlete, then using the mean to get the 5’3” average is the equivalent of stretching the truth. In this case, the real answer would require us to use something other than the mean to find the actual average. Since a dwarf is considered to have an adult height of less than 4 '10”, and the average NBA athlete is 6' 5'’ as of 2023, we can, in good conscience, regard the NBA athlete as an outlier in this particular sample. The best method to discover the average in this circumstance is to use the median. We do this by removing values on each end of the distribution until we get the exact middle. So, if the NBA athlete is 6 '5” while the rest of the dwarves are 4’7”, 4’8”, 4’9”, and 4 '10’’, we would get a median of 4' 9" which is a better depiction of the average. The same is true for salary. If the NBA athlete makes over $2,000,000 while the dwarves make under $20,000 a year, then the average is not six figures but five figures. In this scenario, it would have been better to calculate the average based on the median rather than the mean. Someone who would deliberately do otherwise is purposely skewing the data.
There are several ways someone can misuse data to achieve a particular result. One method is data dredging or p-hacking, when one manipulates data analysis to produce statistically significant results. Researchers do this by testing and reporting only those findings that show statistical significance while dismissing those that have null results. This is known as Publication Bias—an unintended but inevitable consequence of science journalism. Typically, journals prefer to report noteworthy findings over those that don’t. Moreover, those findings are cited and promoted more often, which can lead to an increase in false positives.
Why does this matter? For two reasons: Firstly, data dredging creates a flawed image of what the data actually shows, and secondly, it reinforces that image by focusing on the patterns and correlations within the data despite the lack of replicable results. The rules and exceptions do not matter if one’s primary focus is to bring public attention to their work. We must consider the forces of human nature anytime we draw conclusions, or else we will become blinded by science. Remember, anyone can use statistics to say anything if they know how to make it sound convincing. And no one is immune to confirmation bias when interpreting data. Or, as economist Ronald Coase once remarked:
“If you torture the data enough, nature will always confess.” ³ - Ronald Coase
Indeed, we must remain detached from any particular outcomes to discover the truth. Whether or not a rule or exception exists depends on whether or not a result is replicable. If, after testing a hypothesis several times, the results are inconsistent, we cannot in good conscience claim a conclusive answer and must consider other possibilities. Moreover, we must examine any potential conflicts of interest and hidden biases for the sake of scientific integrity. Human nature, especially the study of it, always has a way of going undetected, even by the most diligent researchers. In many cases, they succumb to the worst aspects of it—blind ambition, the desire for attention, the approval of peers, and the receiving of praise that follows. The irony is that in our pursuit to discover what makes us human, we ignore our own nature in the process. However, it is also true that if it weren’t for the positive aspects of human nature, we would have no desire to examine it in the first place. These include curiosity, the desire for mastery, helping others, and pursuing a goal beyond oneself. My hope for the future of research is that we maintain the spirit of the latter and not the former.
The most crucial aspect when determining rules and exceptions is understanding that all information is subject to interpretation. Sometimes, we misinterpret or can be misled by scientific data and, in the process, be fooled into thinking that what is factual is more or less an exaggeration. We must be cautious when making all-or-nothing claims. While it is true that we should remain objective in the pursuit of truth, prematurely taking any absolutist position will surely narrow our perspective. Of course, certain truths, such as mathematics, are axiomatic since we regard them as self-evident. However, some truths regarding human nature are much more complex and multi-faceted. Hence why, research that aims to explain behavior between people is an endeavor that requires the utmost amount of detachment and openness to whatever the results might be. Moreover, it is important to understand that rules and exceptions can change if data to the contrary is statistically significant.
In short, rules exist as a consequence of carefully conducted research that produces replicable results, whereas exceptions exist in relation to whatever the rules are unless evidence proves otherwise. We must not make the mistake of using whataboutisms or personal anecdotes as having equal veracity. Instead, we should study human nature like anything else—by setting our personal agendas aside. Clearly, there are always underlying motivations at play when studying the human condition. Our opinions often reflect our character or upbringing, and when the answers don’t line up with our thinking, they become, in some cases, a threat to our worldview. Therefore, never let yourself become too attached to any particular outcome and dedicate yourself instead to always seeking truth. Then—and only then—will you not be blinded by science and have a clear understanding of what makes a rule and what makes an exception.
